Экспоненциальный рост
Если прирост численности популяции пропорционален количеству особей, численность популяции будет расти экспоненциально.
Выражение «экспоненциальный рост» вошло в наш лексикон для обозначения быстрого, как правило безудержного увеличения. Оно часто используется, например, при описании стремительного роста числа городов или увеличения численности населения. Однако в математике этот термин имеет точный смысл и обозначает определенный вид роста.
Экспоненциальный рост имеет место в тех популяциях, в которых прирост численности (число рождений минус число смертей) пропорционален числу особей популяции. Для популяции человека, например, коэффициент рождаемости примерно пропорционален количеству репродуктивных пар, а коэффициент смертности примерно пропорционален количеству людей в популяции (обозначим его ). Тогда, в разумном приближении,
прирост населения = число рождений — число смертей
или
(Здесь — так называемый коэффициент пропорциональности, который позволяет нам записать выражение пропорциональности в виде уравнения.)
Пусть — число особей, добавившихся к популяции за время
, тогда если в популяции в общей сложности
особей, то условия для экспоненциального роста будут удовлетворены, если
После того как в XVII веке Исаак Ньютон изобрел дифференциальное исчисление, мы знаем, как решать это уравнение для — численности популяции в любое заданное время. (Для справки: такое уравнение называется дифференциальным.) Вот его решение:
где — число особей в популяции на начало отсчета, а
— время, прошедшее с этого момента. Символ
обозначает такое специальное число, оно называется основание натурального логарифма (и приблизительно равно 2,7), и вся правая часть уравнения называется экспоненциальная функция.
|
При экспоненциальном росте скорость увеличения численности популяции повышается до бесконечности. |
Чтобы лучше понять, что такое экспоненциальный рост, представьте себе популяцию, состоящую изначально из одной бактерии. Через определенное время (через несколько часов или минут) бактерия делится надвое, тем самым удваивая размер популяции. Через следующий промежуток времени каждая из этих двух бактерий снова разделится надвое, и размер популяции вновь удвоится — теперь будет уже четыре бактерии. После десяти таких удвоений будет уже более тысячи бактерий, после двадцати — более миллиона, и так далее. Если с каждым делением популяция будет удваиваться, ее рост будет продолжаться до бесконечности.
Существует легенда (скорее всего, не соответствующая действительности), будто бы человек, который изобрел шахматы, доставил этим такое удовольствие своему султану, что тот пообещал исполнить любую его просьбу. Человек попросил, чтобы султан положил на первую клетку шахматной доски одно зерно пшеницы, на вторую — два, на третью — четыре и так далее. Султан, посчитав это требование ничтожным по сравнению с оказанной им услугой, попросил своего поданного придумать другую просьбу, но тот отказался. Естественно, к 64-му удвоению число зерен стало таким, что во всем мире не нашлось бы нужного количества пшеницы, чтобы удовлетворить эту просьбу. В той версии легенды, которая известна мне, султан в этот момент приказал отрубить голову изобретателю. Мораль, как я говорю моим студентам, такова: иногда не следует быть чересчур умным!
Пример с шахматной доской (как и с воображаемыми бактериями) показывает нам, что никакая популяция не может расти вечно. Рано или поздно она попросту исчерпает ресурсы — пространство, энергию, воду, что угодно. Поэтому популяции могут расти по экспоненциальному закону лишь некоторое время, и рано или поздно их рост должен замедлиться. Для этого нужно изменить уравнение так, чтобы при приближении численности популяции к максимально возможной (которая может поддерживаться внешней средой) скорость роста замедлялась. Назовем эту максимальную численность популяции . Тогда видоизмененное уравнение будет выглядеть так:
Когда намного меньше
, членом
можно пренебречь, и мы возвращаемся к первоначальному уравнению обычного экспоненциального роста. Однако когда
приближается к своему максимальному значению
, значение
стремится к нулю, соответственно стремится к нулю и прирост численности популяции. Общая численность популяции в этом случае стабилизируется и остается на уровне
. Кривая, описываемая этим уравнением, а также само уравнение, имеют несколько названий — S-кривая, логистическое уравнение, уравнение Вольтерры, уравнение Лотки—Вольтерры. (Вито Вольтерра, 1860–1940 — выдающийся итальянский математик и преподаватель; Альфред Лотка, 1880–1949 — американский математик и страховой аналитик.) Как бы она ни называлась, это — достаточно простое выражение численности популяции, резко возрастающей экспоненциально, а затем замедляющейся при приближении к некоему пределу. И она гораздо лучше отражает рост численности реальных популяций, чем обычная экспоненциальная функция.
Отношения хищник—жертва
Отношения между хищниками и их жертвами развиваются циклически, являясь иллюстрацией нейтрального равновесия.
Иногда простая математическая модель хорошо описывает сложную биологическую систему. Примером этого служат долговременные отношения между видами хищника и жертвы в какой-либо экосистеме. Математические расчеты роста популяции отдельно взятого вида (см. выше) показывают, что пределы плотности популяции можно описать простыми уравнениями, которые на выходе дают характерную S-образную кривую. Это — кривая численности популяции, которая растет экспоненциально, пока она небольшая, а затем выравнивается, когда она достигает пределов возможности экосистемы поддерживать ее. Простое продолжение этой концепции позволяет нам понять экосистему, в которой взаимодействуют два вида — хищник и жертва.
Итак, если число растительноядных жертв , а число плотоядных хищников
, то вероятность, что хищник встретится с травоядным, пропорциональна произведению
. Другими словами, чем выше численность одного из видов, тем выше вероятность таких встреч. В отсутствие хищников популяция жертвы будет расти экспоненциально (по крайне мере вначале), а в отсутствие жертв популяция хищника сократится до нуля — либо из-за голода, либо в результате миграции. Теперь, если
— изменение популяции растительноядных за время
, а
изменение популяции плотоядных за тот же интервал времени, то две популяции описываются уравнениями:
и
Здесь — скорость роста численности травоядных в отсутствие хищников, а
— скорость сокращения численности плотоядных в отсутствие травоядных. Постоянные
и
— скорость, с которой встречи хищников с жертвами удаляют травоядных из популяции, и скорость, с которой эти встречи позволяют хищникам прибавлять численность своей популяции. Знак минус в первом уравнении показывает, что встречи сокращают популяцию жертвы, а знак плюс во втором говорит о том, что встречи увеличивают популяцию хищника. Как видите, любое изменение численности травоядных влияет на численность плотоядных, и наоборот. Две популяции необходимо рассматривать вместе.
|
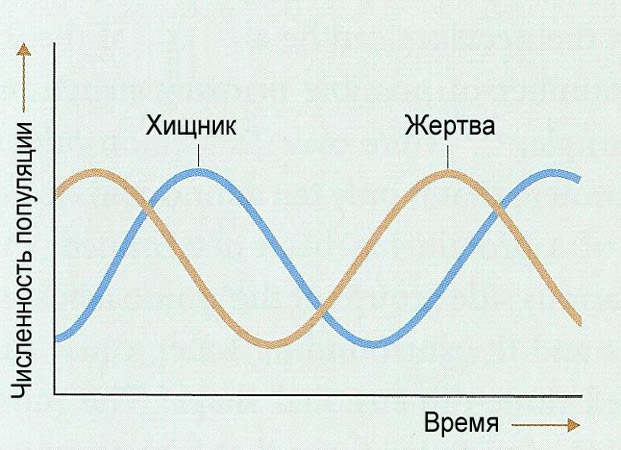
Циклические изменения численности видов хищника и его жертвы. |
Решение этих уравнений показывает, что обе популяции развиваются циклически. Если популяция травоядных увеличивается, вероятность встреч хищник—жертва возрастает, и, соответственно (после некоторой временной задержки), растет популяция хищников. Но рост популяции хищников приводит к сокращению популяции травоядных (также после некоторой задержки), что ведет к снижению численности потомства хищников, а это повышает число травоядных и так далее. Эти две популяции как бы танцуют вальс во времени — когда изменяется одна из них, за ней следом изменяется и другая.
Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания».
Джеймс Трефил — профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.